| Modelo | Anual | Trimestral | Mensal |
|---|---|---|---|
| Regressão Linear | ✓ | ✓ | ✓ |
| Random Forest | ✗ | ✗ | ✓ |
| SARIMA | ✗ | ✗ | ✓ |
| Suavização Exponencial | ✗ | ✗ | ✓ |
1 Introdução
O presente cenário mundial acerca de mortes e lesões relacionadas à sinistros de trânsito apresenta sérios desafios à saúde pública global, e as tendências evidenciadas pelos dados atuais indicam que esta realidade deve perdurar pelo futuro próximo (WORLD HEALTH ORGANIZATION, 2023). Sendo uma das causas de mortes mais comuns no mundo, as ocorrências de sinistros de trânsito afetam principalmente pedestres, ciclistas e motociclistas, além de induzir severos danos materiais, tanto em questão de propriedade particular quanto pública. Isto estimula países a buscarem métodos estimativos sobre os efeitos sociais, econômicos e epidemiológicos da taxa de mortes no trânsito e como se traduzem em custos e perdas na produtividade da sociedade em geral (RODRÍGUEZ; JATTIN; SORACIPA, 2020).
A segurança viária pode ser um indicador da situação de desenvolvimento de uma região, visto que é uma característica do desempenho da mobilidade urbana. Entende-se que as mortes no trânsito dependem de diversos fatores estruturais, socioeconômicos e ambientais do contexto urbano (ZHONG-XIANG et al., 2014), o que implica que elevadas taxas de sinistros viários colaboram no diagnóstico de problemas da mobilidade e saúde pública em geral, despertando o debate político sobre a regulamentação das normas viárias e apontando a carência da sociedade em combater estes eventos.
Apesar da crescente adesão por itens de segurança veicular, os sinistros de trânsito permanecem como um problema de saúde pública, já que fazem parte de um agravo que repercute por toda a sociedade (ANDRADE; ANTUNES, 2019), sendo a décima segunda maior causa de óbitos em todas as faixas etárias e a principal entre indivíduos de 5 a 29 anos (WORLD HEALTH ORGANIZATION, 2023). Como previsto por modelos estatísticos prévios à 2020 (BLUMENBERG et al., 2018), o Brasil apresentou baixo desempenho em cumprir a meta estabelecida pela Primeira Década de Ações pela Segurança no Trânsito. Neste cenário, o Plano Nacional de Redução de Mortes e Lesões no Trânsito (PNATRANS) foi desenvolvido para guiar as ações pela mobilidade segura nacional durante o período da Segunda Década de Ação pela Segurança no Trânsito (MINISTÉRIO DA INFRAESTRUTURA, 2018), na intenção de aprimorar o desempenho da segurança viária em relação a década passada, se alinhando aos Objetivos de Desenvolvimento Sustentável estabelecidos pela Agenda 2030 da Organização das Nações Unidas (ONU). Para atingir tais metas, o Art. 3º da Resolução Contran Nº 1004, de 21 de dezembro de 2023, relata que o PNATRANS se apoia em seis principais pilares (CONSELHO NACIONAL DE TRÂNSITO, 2023):
Gestão da Segurança no Trânsito;
Vias Seguras;
Segurança Veicular;
Educação para o Trânsito;
Vigilância, Promoção da Saúde e Atendimento às Vítimas no Trânsito e;
Normalização e Fiscalização.
Em relação à Resolução Contran N° 870, de 13 de setembro de 2021 (CONSELHO NACIONAL DE TRÂNSITO, 2018), a N° 1004 ratifica o quinto pilar, expandindo a visão de atendimento às vítimas no trânsito. A resolução mais recente ainda adiciona ao PNATRANS os princípios e diretrizes que constituem um sistema seguro de mobilidade, aprofundando os conceitos de iniciativas, ações e produtos promovidos pelos órgãos do Sistema Nacional de Trânsito para cada pilar.
A busca pela fundamentação técnica para a proposição de políticas públicas a respeito da mobilidade segura fomenta o estudo de diversas categorias de modelos preditivos para a sinistralidade no trânsito, tanto para estimar o número de ocorrências quanto para avaliar a influência das variáveis consideradas sobre a ocorrência de sinistros fatais. Em geral, a literatura pertinente apresenta alguns meios distintos para alcançar estes modelos de melhor ajuste: Modelos lineares multivariados foram ajustados para extrair tendências sobre os critérios aferidos (BLUMENBERG et al., 2018; CAI; ZHU; YAN, 2015), assim como modelos preditivos baseados em cadeia de Markov (JIN; ZHENG; GENG, 2020; SENETA, 1996). Outras abordagens utilizam técnicas de análise de séries temporais, utilizando métodos autoregressivos como o ARIMA - Modelo Auto-Regressivo Integrado de Médias Móveis (AL-GHAMDI, 1995) e redes neurais artificiais (JAFARI et al., 2015).
O presente documento está organizado com a seguinte estrutura: a Seção 2 inclui os objetivos principais e complementares do trabalho; a Seção 3 apresenta a metodologia aplicada no trabalho, juntamente com a coleta de dados e explicação sobre os modelos aplicados; a Seção 4 traz os resultados dos modelos preditivos aplicados, a Seção 5 apresenta a estimativa de custo dos óbitos e por fim, a Seção 6 conclui o trabalho.
2 Objetivos
Considerando o presente cenário, este estudo tem como objetivo elaborar um modelo de aprendizado de máquina para a previsão de mortes no trânsito em âmbito nacional no Brasil, investigando dados socioeconômicos e estruturais com o propósito de explorar diversos tipos de tratamentos e análises estatísticas para criar perspectivas futuras a cerca do cenário brasileiro da segurança viária. Posto isso, o projeto ainda visa avaliar a qualidade de cada tipo de modelo experimentado em expressar o fenômeno dos óbitos no trânsito, assim como elucidar a influência e relevância de cada variável considerada na construção do modelo preditivo criado para a incidência destes eventos.
Outro objetivo do trabalho é realizar o cálculo do custo financeiro dos óbitos no trânsito brasileiro, utilizando como base o valor previsto pelo modelo para 2023 e com base nas estimativas do Instituto de Pesquisa Econômica Aplicada (IPEA).
O código-fonte do trabalho está disponibilizado para acesso em um repositório no perfil do GitHub do Observatório Nacional de Segurança Viária.
3 Metodologia
3.1 Coleta de dados
A coleta de dados foi efetuada considerando as principais variáveis teoricamente relacionadas à mortalidade no trânsito disponíveis ao público, amparando a escolha de cada grandeza na literatura previamente revisada. Estes dados são reunidos e pré-processados para a formação de conjuntos específicos para cada método de modelagem, variando com a resolução temporal de cada abordagem (anual, trimestral e mensal).
Dito isto, investigam-se diversas bases de dados a fim de compilar e extrair estas informações para uma análise preliminar, anterior à modelagem. Entre as fontes contempladas estão:
PIB mensal, fornecido pelo Sistema Gerenciador de Séries Temporais do Banco Central (BANCO CENTRAL DO BRASIL, 2023), mensurado em dólares;
População nacional residente, fornecida pelo sistema DataSUS do Ministério da Saúde (MINISTÉRIO DA SAÚDE, 2023a), obtida pelo sistema TABNET;
Sinistros em rodovias federais, fornecidos pelo portal de dados abertos da Polícia Rodoviária Federal (POLÍCIA RODOVIÁRIA FEDERAL, 2023);
Condutores habilitados, fornecidos pelo portal de estatísticas da Secretaria Nacional de Trânsito (Senatran), provenientes do Registro Nacional de Condutores Habiltados (RENACH) (MINISTÉRIO DOS TRANSPORTES, 2023a);
Frota veicular, fornecida pelo portal de estatísticas da Senatran, provida pelo Registro Nacional de Veículos Automotores (RENAVAM) (MINISTÉRIO DOS TRANSPORTES, 2023b);
Óbitos em sinistros de trânsito, fornecidos pelo Sistema de Informação de Mortalidade (SIM) do DataSUS (MINISTÉRIO DA SAÚDE, 2023b), obtidos com auxílio da biblioteca
microdatasus(SALDANHA, 2023) da linguagem de programação R.
Vale ressaltar que nem todos os dados estão disponíveis em todas as escalas de tempo estudadas, por isso não foram inclusas no processo de criação de certos modelos. As bases de condutores habilitados e população residente, por exemplo, são unicamente anuais, impossibilitando sua utilização no modo trimestral e mensal.
3.2 Modelos
3.2.1 Escalas de tempo
Em razão da indisponibilidade de dados, os modelos confeccionados em geral contemplam uma janela de tempo de 2011 até a atualidade (2023), sendo as principais unidades de tempo estudadas a anual, trimestral e mensal. Ao criar modelos de série temporal, deve-se notar que a abundância de dados a serem modelados tem uma relação direta com a capacidade do modelo de aprender e conseguir expressá-los em instantes futuros.
Modelos treinados em âmbito mensal conseguem emitir previsões todo mês, porém perdem precisão quanto mais adiante realizam previsões, enquanto modelos anuais podem predizer com alto desempenho os valores de anos posteriores, mas não são capazes de prever meses ou trimestres. Assim, estas diversas abordagens são testadas a fim de comparar os desempenhos e utilidades de cada método.
3.2.2 Análise de Série Temporal x Análise Determinística
É importante ressaltar que há mais de uma maneira de se entender as relações entre os dados e, portanto, mais de uma maneira de interpretá-los em questão do processo de modelagem do problema em mãos. Neste sentido, as metodologias propostas a partir da observação dos dados disponíveis implicam duas possíveis linhas de raciocínio de análise estatística: a análise de série temporal e a análise de regressão, ou determinística.
A análise de série temporal se apoia no conceito de séries temporais: um conjunto de dados de alguma grandeza ordenada em sequência cronológica. Logo, seu propósito é criar um modelo generalista que prevê as observações futuras baseado nas ocorrências passadas. Este tipo de modelagem assume que o que ocorre no momento atual, neste caso os óbitos no trânsito, possui relação com o que ocorreu anteriormente. O modelo também leva em consideração o comportamento ao longo do tempo, como sazonalidade, tendência e heteroscedasticidade, e é altamente dependente da autocorrelação.
Já a análise de regressão tem como base a criação de um modelo de variáveis preditadas (ou dependentes) que dependem de variáveis preditivas ou preditoras (independentes), criando uma função generalista que expressa a relação destas categorias de variáveis entre si. Diferentemente da análise temporal, a regressão independe da sequência cronológica dos fatos, mas é diretamente afetada pela correlação das variáveis independentes com a variável dependente que se deseja prever.
À vista disso, o processo de modelagem pretende essencialmente englobar estas duas principais metodologias de análise de dados, criando modelos de ambas as categorias. Conforme o embasamento teórico acerca da segurança viária, estas modelagens são possíveis pelo fato de que o fenômeno das mortes no trânsito possui tanto uma correlação expressiva com variáveis externas quanto um comportamentos temporal bem ordenado.
3.2.3 Configurações
Modelos estatísticos e de aprendizado de máquina constituem um grandioso conjunto de ferramentas e métodos matemáticos e computacionais para expressar fenômenos naturais por meio de funções e algoritmos. Visando expressar as dinâmicas dos óbitos ocasionados pelo transporte, o primeiro método escolhido por sua simplicidade e versatilidade é a regressão linear, norteada pelo conceito de correlações lineares entre diferentes grandezas numéricas.
Como discutido em JAMES et al. (2021), a regressão linear simples se enquadra como um método estatístico e de aprendizado de máquina que se baseia na relação de uma variável dependente quantitativa \(Y\) em função de uma variável independente quantitativa \(X\), com \(\epsilon\) representando uma variável aleatória sobre o erro associado à estimativa, demonstrando a relação matemática linear entre as grandezas:
\[ Y = \beta_0 + \beta_1X + \epsilon \]
Desta forma, pode-se prever uma imagem \(Y\) ao se injetar um valor em \(X\) na equação, dado que estas variáveis tenham uma correlação linear significativa e que os ditos coeficientes ou parâmetros \(\beta_0\) e \(\beta_1\) sejam estimados para este modelo. No contexto deste projeto, o objetivo é estimar um modelo capaz de predizer o número de vítimas em relação a mais de uma variável independente, tratando-se então de uma regressão linear múltipla:
\[ Y_i = \beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_nX_n + \epsilon \]
Neste estudo, esta técnica de regressão é amplamente utilizada em todas as resoluções temporais em razão de sua facilidade de explicação e pelas altas correlações lineares entre as variáveis. Estas correlações estatísticas são expressas em índices numéricos pelas técnicas de correlação linear (de Pearson) e correlação de Spearman, como visto na Figura 16. Sendo assim, serão apresentados os modelo lineares anual, trimestral e mensal confeccionados com este método.
Adiante, é esperado que alguns tipos de modelos necessitem de uma quantidade maior de dados disponíveis para obterem resultados significantes. Modelos autorregressivos são univariados, e necessitam de um conjunto extenso e “limpo” de observações para serem adequadamente ajustados, enquanto modelos regressivos mais complexos, como o Random Forest, são propensos a sobreajuste se não treinados e testados devidamente, algo que representa uma dificuldade em conjuntos de dados reduzidos.
A base de dados extraída com maior número de observações foi a base em resolução mensal, logo os modelos de série temporal SARIMA e Suavização Exponencial, bem como o modelo regressor Random Forest, foram testados apenas no contexto de meses, como indica a Tabela 1. Deste modo, após a regressão linear anual, trimestral e mensal, o modelo Random Forest mensal foi concebido utilizando o mesmo intervalo de dados e variáveis:
De acordo com JAMES et al. (2021), o Random Forest é um método da família de técnicas conhecidas como árvores de decisão que se baseiam em algoritmos que segregam os dados em estratos ou ramos, separando os dados conforme regras de decisão previamente estabelecidas pelo método. Assim, estas árvores “crescem” com base na necessidade do algoritmo em otimizar o processo de divisão dos dados em conjunto menores para melhor expressá-los. O resultado deste algoritmo é uma função estatística que irá retornar um valor previsto com base nas regras de decisões impostas em cada variável preditiva.
flowchart TD
1[Nó Inicial] --> 2(Nó de decisão)
1 --> 3(Nó de decisão)
3 --> 4(Nó de decisão)
4 --> f5[Nó final]
4 --> f6[Nó final]
3 --> f3[Nó final]
2 --> f1[Nó final]
2 --> f2[Nó final]
O Bagged Trees é uma evolução da árvore de decisões convencional, onde diversas árvores são construídas simultaneamente com diversos conjuntos de reamostragem aleatória ajustados paralelamente (técnica de bagging), sendo a média do resultado de todas as árvores o resultado final da predição. O Random Forest é um algoritmo que vai além do Bagged Trees: além da criação de múltiplas árvores simultaneamente, ele também faz aleatoriamente a reamostragem das variáveis preditivas, selecionando conjuntos diferentes de variáveis para cada árvore. Isto serve para descorrelacionar estes atributos, já que altas correlações entre preditivas podem enviesar o modelo final, mostrando que o Random Forest é um algoritmo que pratica seleção de atributos internamente.
Diversas técnicas de aprendizado de máquina requerem valores pré-estabelecidos de hiperparâmetros para o treinamento. Neste caso, este tipo de modelo requer valores iniciais para o número de árvores que se deseja treinar (parâmetro trees) e o número de atributos que se deseja reamostrar para cada árvore (parâmetros mtry). Estes valores foram arbitrariamente escolhidos como 5000 e 5 respectivamente neste estudo, mas outra possível abordagem seria a otimização de hiperparâmetros, utilizando técnicas como grid search.
Em seguida, o estudo é dirigido à análise de série temporal, iniciando pelo modelo SARIMA (Seasonal Autoregressive Integrated Moving Average*). Como relatado em SHUMWAY; STOFFER (2017), este é um método da família ARMA, mais especificamente uma alteração do método ARIMA, conhecido por reduzir ou remover completamente a componente sazonal de uma série temporal univariada. O modelo ARIMA possui três parâmetros que espelham as componentes no seu nome: \(p\) para a autoregressão (AR), \(d\) para diferenciação (I) e \(q\) para média móvel (MA), criando o algoritmo \(Arima(p, d, q)\).
A autoregressão é simplesmente uma variação da regressão linear que utiliza de valores anteriores à observação presente como variáveis preditivas invés de outra grandeza, construindo um modelo univariado que gera previsões baseadas em valores prévios. A diferenciação, como citada no parágrafo anterior, visa remover a sazonalidade, enquanto a componente de média móvel têm o objetivo de atualizar a predição conforme a tendência da média. A alteração do modelo SARIMA em relação ao último seria a adição de três novos parâmetros para gerar um ARIMA específico para a componente sazonal da série temporal, assim como um quarto componente \(m\) para a periodicidade, tornando a fórmula \(Sarima(p,d,q)(P,D,Q)m\).
O último método utilizado foi a Suavização Exponencial de Holt-Winters, ou Suavização Exponencial Tripla. Este método é basicamente uma aplicação de filtragem de sinais, visando aproximar uma função matemática generalista sobre uma série ruidosa para melhor interpretar seu comportamento. Este alisamento da série resulta em um modelo simples, mas que pode ser tão eficaz em prever novas observações quanto um modelo ARMA, dependendo da sazonalidade do conjunto de dados.
4 Resultados
4.1 Análise Exploratória de Dados
Os conjuntos de dados extraídos e pré-processados em função das unidades de tempo denunciam os comportamentos de cada atributo em relação a passagem dos anos, trimestres e meses. Em destaque, os óbitos servem como um dos principais indicadores da qualidade e disseminação dos sistemas de segurança viária do país, mostrando a evolução das mortes ao longo do tempo:
Os gráficos de óbitos no trânsito levantam uma tendência crescente nas vítimas fatais nos últimos três anos. O ano de 2019 aintgiu a menor quantidade de óbitos relacionadas ao trânsito nos últimos 10 anos, quando em 2020 a têndencia tornou a crescer. No ano de 2021 houveram 33.813 vítimas fatais, aproximadamente 2000 a mais que em 2019. Em 2022, essa tendência foi levemente atenuada, mantendo um número similar de óbitos em relação ao ano anterior.
Assim sendo, os demais atributos do conjunto de dados podem ser visualizados em função do tempo, como foi feito para o caso da variável preditada, com o intuito de destacar cada variável preditiva ao longo dos períodos disponíveis:
Observa-se uma diferença entre os comportamentos de cada atributo ao longo do tempo. Variáveis convencionalmente cumulativas como a frota, a população e o número de condutores habilitados dispõem de um crescimento aproximadamente linear por todo o período de estudo. Todavia, detecta-se que a contagem da população se comportou de forma inesperada em alguns anos. Isso pode representar a diferença entre a população censitária e a população estimada pelo IBGE.
Os dados de rodovias federais flutuam de forma análoga aos óbitos no trânsito, agindo como referência do desempenho da segurança viária em nível nacional de determinado período, com uma sazonalidade pronunciada. Estes dados também mostram claramente como os óbitos são eventos incomuns em comparação à quantidade de sinistros totais observados. Porém, enquanto a quantidade de sinistros pode variar intensamente ao longo dos anos, o número de óbitos permanece relativamente constante, com uma redução ao longo da janela de tempo analisada.
O PIB é o atributo com o comportamento mais particular ao longo do tempo em relação às outras variáveis. Foi utilizado o dólar americano em lugar do real brasileiro a fim de observar a oscilação da moeda em um contexto global e revelar a contribuição histórica da economia nacional. Modelos realizados por BLUMENBERG et al. (2018) e ZHONG-XIANG et al. (2014) utilizam do PIB como um indicador do desempenho socioeconômico do país.
4.2 Correlação
O sucesso da modelagem é inteiramente dependente da intensidade e do tipo de relação estatística que as variáveis possuem entre si. Como anteriormente citado, a regressão linear múltipla bem ajustada infere que as preditivas possuem uma correlação linear forte com a preditora, mas um modelo com baixo desempenho não é necessariamente uma evidência de baixa correlação.
Grandezas que variam juntas em uma correlação linear são ditas colineares, e o fenômeno da colinearidade entre variáveis preditivas pode vir a ocasionar sobreajuste ao modelo. Por isso, é necessário avaliar as correlações não lineares, como apontam os correlogramas, a partir do método de correlação Spearman, nas três escalas temporais:
Em todos os correlagramas se encontram valores significativos para praticamente todas as variáveis, sendo que as matrizes de 𝑝-valores calculadas rejeitam a hipótese nula com facilidade para todos os atributos em todas as escalas de tempo.
4.3 Taxas de óbitos
O diagnóstico da segurança no trânsito de uma uma região em um determinado intervalo de tempo é um dos principais tópicos no campo da mobilidade segura, visto que as variáveis que influenciam a saúde no trânsito não são um consenso acadêmico absoluto. Este fato fomenta a pesquisa e desenvolvimento de novas metodologias e indicadores específicos para a análise estatística do cenário brasileiro que melhor interpretem os dados disponíveis e representem o fenômeno real da sinistralidade de maneira verossímil. FERRAZ et al. (2023) disserta sobre a questão da quantificação e qualificação da sinistralidade por meio da determinação de índices utilizando das mortes, população e frota como parâmetros para estabelecer valores representativos do nível de segurança do local.
Estes índices são usualmente referidos em função de altas casas decimais para salientar a significância dos valores de cada taxa calculada. As taxas que direcionaram o presente estudo na avaliação da sinistralidade anual foram as vítimas fatais por 100 mil habitantes e vítimas fatais por 10 mil veículos, como indicado:
As duas taxas anunciam tendências distintas a cerca da fatalidade no trânsito brasileiro. Enquanto o índice de mortes por veículos oferece uma perspectiva de estabilização no número de vítimas, a taxa de habitantes corrobora à visão de que as mortes estão inclinadas ao aumento na década atual. Deve-se levar em consideração que esta diferença de comportamente pode resultar da evolução da frota veicular e da população nacional em intensidades distintas.
4.4 Resultados dos modelos
A avaliação de desempenho de cada modelo foi feita a partir da necessidade e especificações de cada caso. Visualizações podem ser criadas para todos os modelos a fim de apresentar a proximidade das previsões em relação aos valores reais, com métricas de erros sendo utilizadas para quantificar a taxa de acertos de cada modelo. Nota-se que em modelos com maior disponibilidade de dados (trimestral e mensal) foi efetuada a repartição de amostras em conjuntos de treino e teste.
A repartição visa dividir as amostras com uma proporção de 75% dos dados para o treinamento dos modelos, sendo o restante utilizado na validação das previsões pelo cálculo do Erro Quadrado Médio Absoluto (Root Mean Squared Error - RMSE), Erro Médio Absoluto (Mean Squared Error - MAE) e o 𝑅2, ou coeficiente de determinação. A técnica de repartição de treino e teste é consideravelmente mais simples que o método de Cross validation comumente utilizado em modelos de aprendizado de máquina mais robustos, mas pode ser mais adequada a databases menores. Neste estudo, a validação cruzada não influenciou na performance dos modelos e foi abandonada devido ao gasto computacional desnecessário. Já no caso do modelo anual, que possui um conjunto ainda menor de dados, a repartição ou reamostragem é inviável e a validação foi dada com o mesmo conjunto utilizado no treinamento.
4.4.1 Regressão Linear Múltipla
A análise de regressão linear múltipla foi a abordagem mais extensamente utilizada durante a produção do estudo, podendo ser dividida entre as escalas temporais anual, trimestral e mensal. Cada métrica e modelo são extraídos e apresentados para avaliação das suas performances, com os resultados segregados por unidade de tempo.
4.4.1.1 Anual
Para o caso da análise anual, as previsões emitidas são comparadas com as ocorrências reais, enquanto as métricas são baseadas no mesmo conjunto de ajuste do modelo:
| Métrica | Valor |
|---|---|
| RMSE | 707,61 |
| MAE | 668,47 |
| R² | 0,98 |
Como é demonstrado pelo amplo intervalo de confiança preditado (área em cinza no gráfico), o fato do conjunto de dados anuais ser relativamente pequeno confere uma incerteza atribuída à essa abordagem. Para 2023, o modelo prevê 34.631 óbitos no trânsito brasileiro, uma diferença de 737 vítimas e um aumento de aproximadamente 2,1% em relação ao valor real do ano anterior (2022).
As métricas RMSE e MAE são melhor aplicadas de forma comparativa entre diferentes ajustes, sendo utilizados para auxiliar na seleção de atributos para o treinamento do modelo. Foi concluído que as melhores variáveis para explicar as ocorrências de óbitos no trânsito para esta categoria de modelo foram a frota total, os sinistros totais e fatais em rodovias federais e os condutores habilitados.
Como este modelo em específico possui maior variedade de atributos, a combinação de diversas configurações das variáveis preditivas foi feita manualmente para filtrar as de maior utilidade. Componentes como a população, o PIB e as mortes em rodovias federais foram considerados muito colineares, prejudicando a performance do modelo. Na Tabela 3, estão explicitados os melhores atributos e seus coeficientes:
| Variável | Coeficientes | P-valor |
|---|---|---|
| Intercepto Y | 37542.33 | 0.00 |
| Frota | 7214.08 | 0.35 |
| Sinistros fatais | 8525.89 | 0.03 |
| Sinistros | -3804.87 | 0.30 |
| Condutores | -7205.39 | 0.37 |
4.4.1.2 Trimestral
Os dados utilizados foram obtidos por meio do agrupamento trimestral dos dados mensais, sendo constituída uma base de dados específica para o ajuste deste modelo de regressão. As métricas e visualizações para avaliação da performance foram as mesmas do modelo anual, porém, a partir deste, todos os próximos modelos são reamostrados em conjuntos de treino e teste para a validação adequada:
| Métrica | Valor |
|---|---|
| RMSE | 204,66 |
| MAE | 174,97 |
| R² | 0,96 |
O grafico da Figura 22 espelha visualmente a periodicidade e sazonalidade trimestral da mortalidade no trânsito, revelando a existência de épocas de maior risco no trânsito em todos os anos, independente da tendência da série temporal de óbitos. Como esperado, a maior disponibilidade de dados resulta em alterações positivas nas métricas de erros em relação à escala temporal anual.
4.4.1.3 Mensal
A escala mensal é a menor unidade temporal abordada para o estudo e permite observar a sazonalidade dos sinistros:
| Métrica | Valor |
|---|---|
| RMSE | 131,81 |
| MAE | 102,67 |
| R² | 0,91 |
Uma das características notáveis deste modelo é sua capacidade de descrever observações anômalas ao decorrer dos anos, onde os óbitos ultrapassam os intervalos de confiança estipulados pelo modelo, mesmo que este apresente uma alta performance e capacidade preditiva segundo as métricas.
4.4.2 Regressor Random Forest
O segundo modelo utilizado para a análise de regressão, como anteriormente explicado, foi o Regressor Random Forest, ajustado apenas para o contexto mensal. Esta técnica dispensa a seleção de atributos manual que fora necessária para o caso da regressão linear, já que possui um algoritmo seletor interno. Sendo assim, este modelo é treinado e validado no mesmo conjunto mensal anteriormente processado:
| Métrica | Valor |
|---|---|
| RMSE | 120,37 |
| MAE | 94,31 |
| R² | 0,91 |
O Random Forest se sobressai visualmente no gráfico de valores previstos sobre valores reais, visto que as previsões aparentam se aproximar mais à linha de convergência em relação ao modelo anterior. Apesar da incapacidade do algoritmo em gerar intervalos de confiança, o Random Forest raramente estima valores anômalos, apontando que é menos sensível a outliers. Como mencionado na descrição teórica deste algoritmo, este efeito é associado a reamostragem que o modelo faz enquanto está construindo as “árvores” pela técnica bagging, reduzindo o enviesamento dos valores discrepantes.
4.4.3 SARIMA
Após as análises regressivas, a próxima abordagem estátistica estudada é a análise de séries temporais univariadas, sobretudo iniciada pela condução de experimentos utilizando do método SARIMA. Entretanto, antes da modelagem propriamente dita, algumas evidências podem ser reunidas para indicar a viabilidade destes métodos temporais, como a decomposição da série temporal:
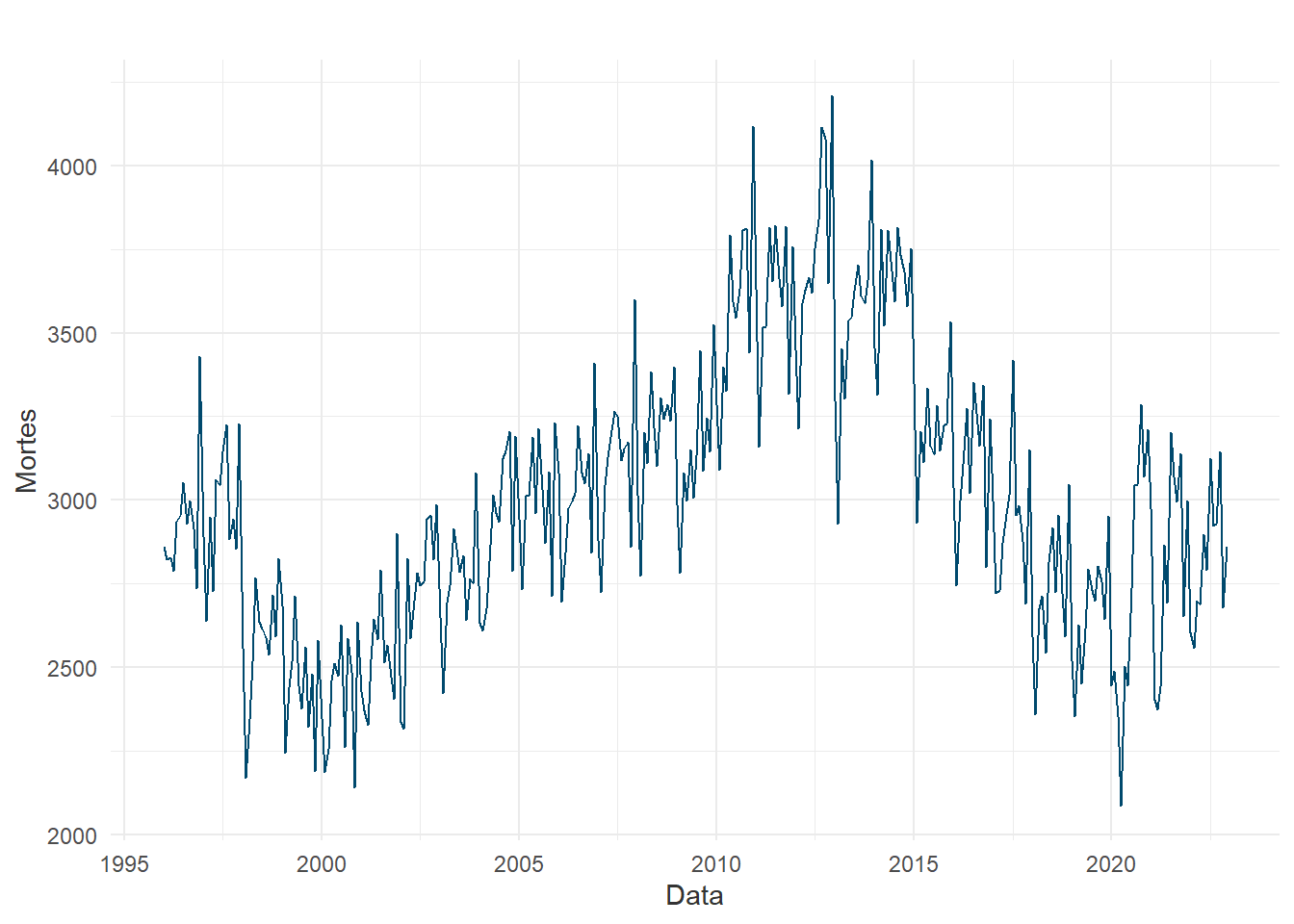
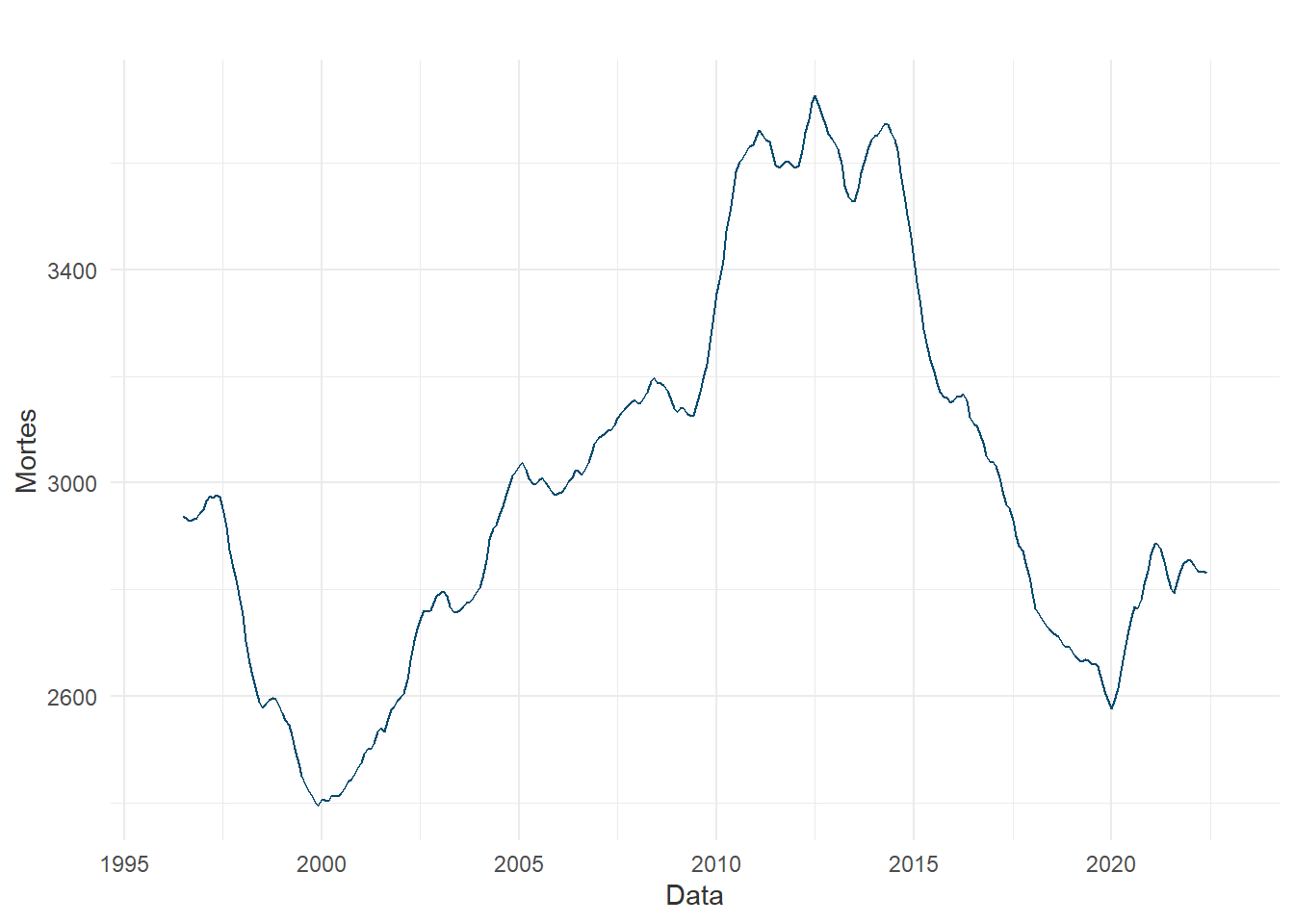
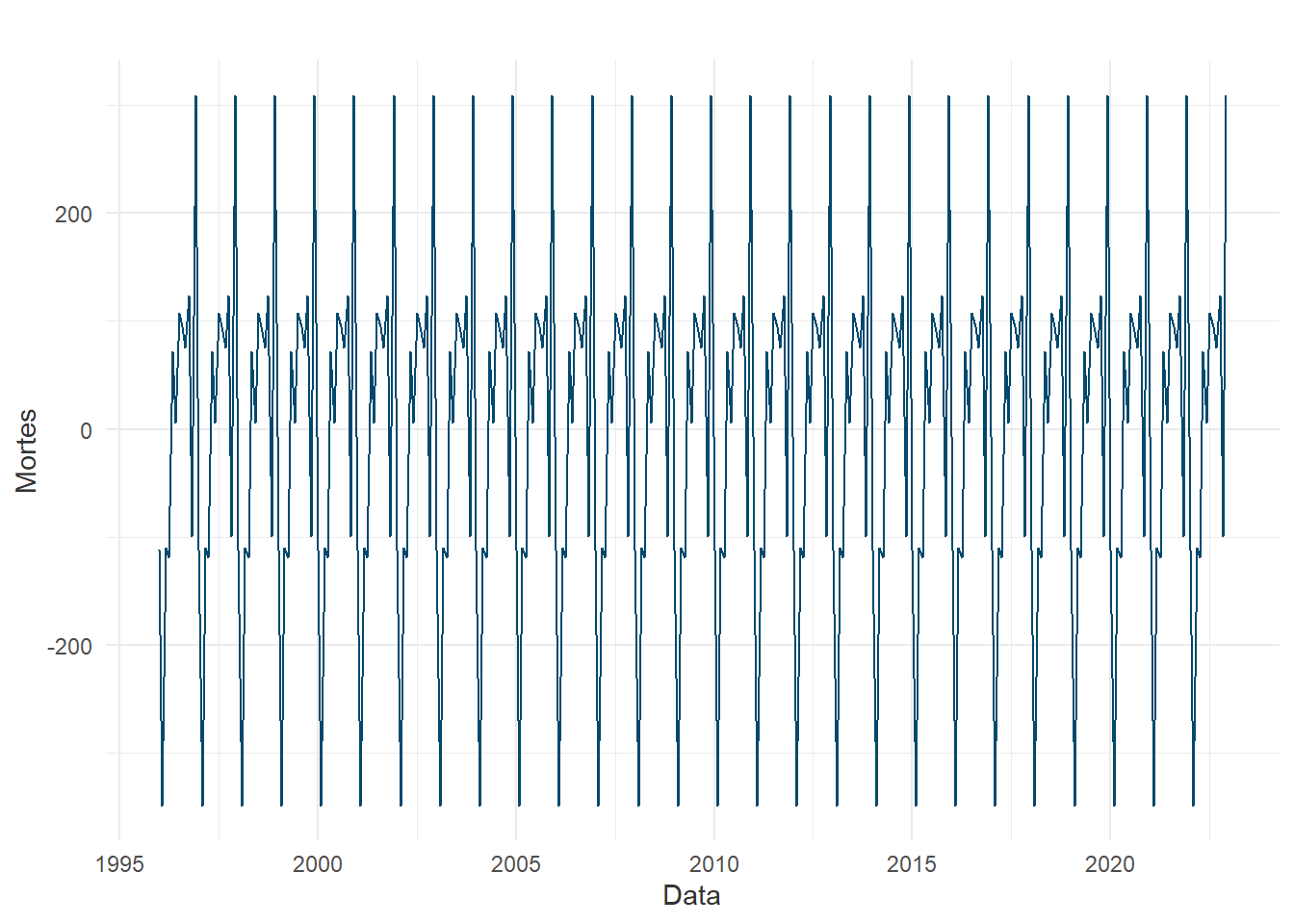
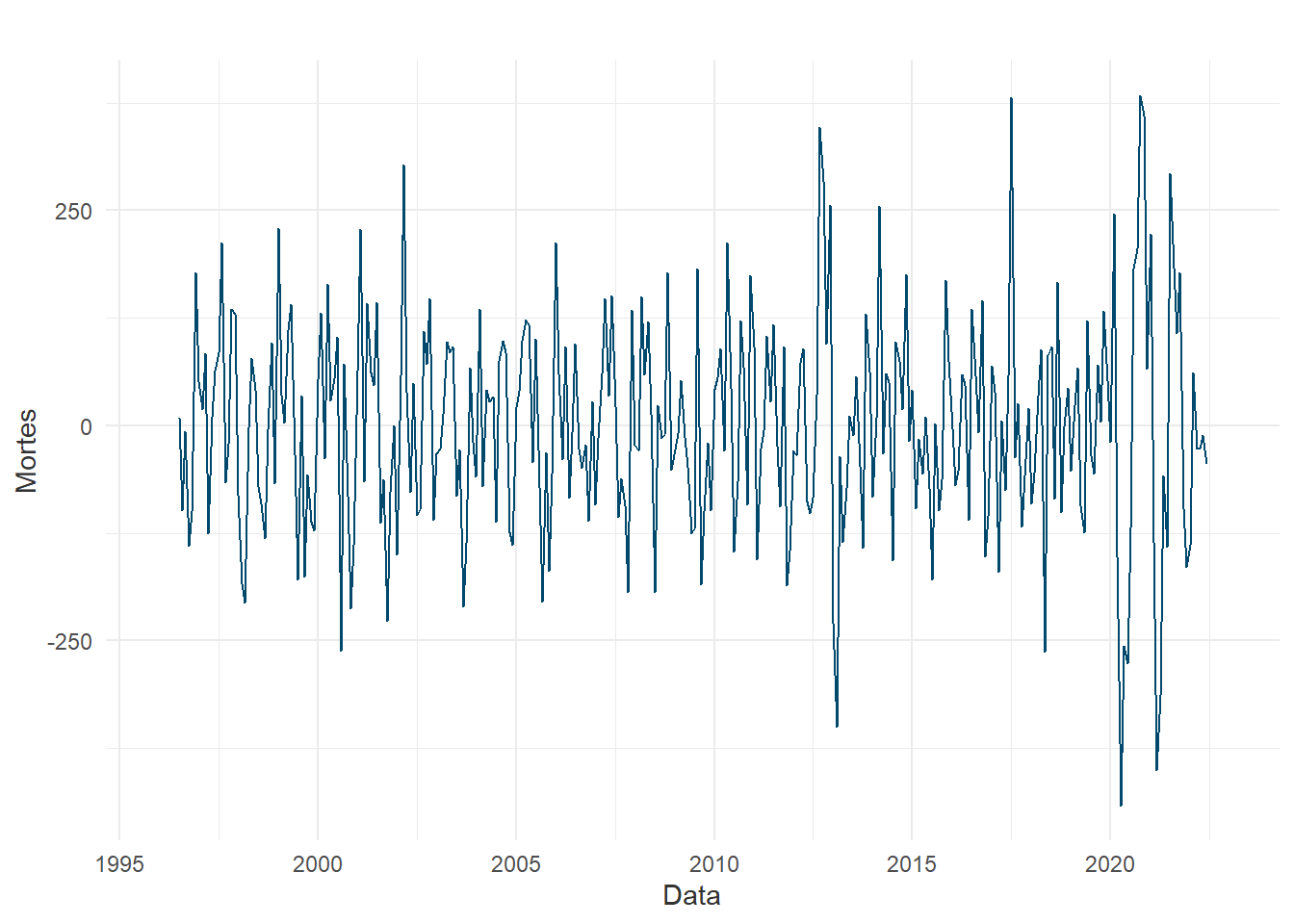
A série decomposta é observada para determinar se o comportamento da quantidade de óbitos ao longo do tempo é característico de uma série modelável pelo SARIMA. A tendência é um forte indicativo de que há uma média móvel neste fenômeno, mas a grande quantidade de resíduo aponta que não há uma sazonalidade tão bem estabelicida e cíclica. Assim, outros métodos usados para o entendimento da sinistrilidade no tempo são os gráficos ACF (Fator de Autocorrelação) e PACF (Fator de Autocorrelação Parcial):
Desta maneira, atenta-se que os dados possuem altas correlações com diversos períodos de lag de forma indireta e direta. Em especial, a quantidade de óbitos em um certo mês aparenta estar profundamente relacionada ao número de óbitos no mesmo mês no ano anterior, visto que há uma alta correlação no lag de 12 meses para ambos os gráficos.
Estas análises são úteis para a decisão manual de valores iniciais para os parâmetros do SARIMA. Todavia, outra forma mais adequada e automatizada de chegar ao ajuste ideal para o modelo é a função de ajuste automático auto.arima() do pacote forecast (HYNDMAN; KHANDAKAR, 2008), uma implementação do método que busca a melhor combinação de parâmetros baseado nos critérios de seleção de modelo AIC (Akaike Information Criterion) e BIC (Bayesian Information Criterion).
| Métrica | Valor |
|---|---|
| RMSE | 139,48 |
| MAE | 106,69 |
| R² | 0,89 |
Por ser um modelo autoregressivo univariado, as previsões emitidas pelo SARIMA são ruidosas, produzindo amplos intervalos de confiança. Modelos dessa categoria possuem baixa longevidade visto que seu desempenho diminui conforme a distância da previsão ao conjunto original. Em comparação a modelos determinísticos, não necessitam de outras variáveis para ter resultados e são, em geral, mais simples computacionalmente.
4.4.4 Suavização Exponencial
A Suavização Exponencial Holt-Winters é o segundo modelo de análise de séries temporais estudado, o qual possui uma abordagem teórica distinta do anterior. Sendo um modelo de suavização, este pretende aproximar uma função que filtre a série temporal original e expresse o comportamento dos dados de forma simplificada.
| Métrica | Valor |
|---|---|
| RMSE | 154,28 |
| MAE | 120,24 |
| R² | 0,87 |
Modelos de suavização são ainda mais simples que modelos ARIMA já que constituem métodos de filtragem espectral convencionais. Usualmente, a literatura destaca que modelos autoregressivos são mais adequados para séries temporais ruidosas, enquanto modelos exponenciais respondem melhor à séries sazonais. Outra possível vantagem da exponenciação é sua priorização de dados mais novos, dado que este método reduz o peso de cada observação exponencialmente conforme a distância do valor mais recente (SHUMWAY; STOFFER, 2017).
4.5 Comparação de Modelos
Após os experimentos, a seleção de um modelo final é feita de forma comparativa, considerando não apenas os índices de métricas de erros calculados mas também as características e capacidades de cada modelo individualmente. A Tabela 9 demonstra os valores de desempenho dos modelos:
| Modelo | RMSE | MAE | RSQ |
|---|---|---|---|
| Anual | |||
| Regressão Linear | 707,61 | 668,47 | 0,98 |
| Trimestral | |||
| Regressão Linear | 204,66 | 174,97 | 0,96 |
| Mensal | |||
| Regressão Linear | 131,81 | 102,67 | 0,91 |
| Random Forest Regressor | 120,37 | 94,31 | 0,91 |
| Exponential Smoothing | 154,28 | 120,24 | 0,87 |
| SARIMA | 139,48 | 106,69 | 0,89 |
O RMSE e o MAE melhoram em escalas menores de tempo, sendo consequência indireta da maior disponibilidade de dados para o treinamento do modelo. Mesmo assim, será perceptível que, por exemplo, um modelo mensal bem ajustado não prevê um ano inteiro melhor que um modelo anual, por efeito da acumulação de erros associados às previsões de cada mês. Como implica a Tabela 9, o modelo linear anual aparenta ter resultados mais plausíveis que o mensal, mesmo tendo um desempenho de RMSE e MAE inferior. Em relação ao 𝑅2, o modelo anual apresenta o melhor desempenho.
| Modelo | Previsão | Máx. | Mín. |
|---|---|---|---|
| Linear Anual | 34.631 | 37.516 | 31.747 |
| Linear Trimestral | 36.457 | 39.271 | 33.644 |
| Linear Mensal | 36.766 | 38.746 | 34.785 |
| * RF Mensal | 34.436 | - | - |
| SARIMA Mensal | 32.643 | 35.803 | 29.484 |
| ETS Mensal | 32.812 | 36.127 | 29.498 |
| * Algoritmo não produz intervalo de confiança | |||
Nota-se que ambos os métodos de análise de séries temporais prevêem uma queda, enquanto os modelos regressivos estipulam que as fatalidades crescem. Na Figura 35, os resultados de cada modelo foram agrupados e somados por ano para visualização de cada série temporal individualmente:
Em questão das taxas anteriormente discutidas para quantificação dos óbitos em relação à população e à frota veicular, novos valores podem ser calculados sobre as previsões a fim de averiguar a mudança destas taxas em função do tempo e tipo de modelo:
5 Custos dos óbitos
A presente seção inclui o processo e resultado da estimativa de custos para a quantidade de óbitos prevista para 2023, conforme o modelo linear anual previamente ajustado (34.631 óbitos). Fez-se a estimativa dos custos financeiros com base na estimativa dos custos de sinistros do Brasil elaborada pelo Instituto de Pesquisa Econômica Aplicada (IPEA).
Em 2020, o IPEA divulgou o relatório “CUSTOS DOS ACIDENTES DE TRÂNSITO NO BRASIL: ESTIMATIVA SIMPLIFICADA COM BASE NA ATUALIZAÇÃO DAS PESQUISAS DO IPEA SOBRE CUSTOS DE ACIDENTES NOS AGLOMERADOS URBANOS E RODOVIAS” (CARVALHO, 2020), cujo principal objetivo foi apresentar o resultado das atualizações das pesquisas de custos dos acidentes de trânsito no Brasil.
No trabalho realizado pelo IPEA, a estimativa dos custos dos sinistros é realizada de forma distinta para rodovias federais, rodovias estaduais ou municipais, e aglomerados urbanos. A estimativa para os sinistros ocorridos em rodovias federais é baseada em três componentes: (i) componentes de custos associados às pessoas; (ii) componentes de custos associados aos veículos; e (iii) componentes de custos institucionais e danos patrimoniais (CARVALHO, 2020).
Para o fim de estimar o custo dos óbitos no trânsito brasileiro em 2023, será utilizado o custo associado às pessoas, na categoria “Mortos”. Mesmo que essa seja uma estimativa para rodovias federais, ela será utilizada no calculo dos custos dos óbitos de uma forma geral para a quantidade de óbitos no Brasil em 2023, pois as outras categorias (rodovias estaduais / municipais e aglomerados urbanos) não possuem essa estimativa de componente associado às pessoas. Assim, será possível alcançar uma estimativa aproximada deste custo total.
Os componentes de custos associados às pessoas que foram à óbito por consequência de sinistros de trânsito englobam os custos pré-hospitalares, custos hospitalares, custos de perda de perda de produção e custos de remoção. O IPEA estimou um custo total associado à cada vítima fatal de sinistros de R$ 433.286,69, considerando um valor em reais de dezembro de 2014 (CARVALHO, 2020). Com o objetivo desse atualizar esse valor para dezembro de 2023, utilizou-se o Índice Nacional de Preços ao Consumidor Amplo (IPCA). De acordo com a Calculadora do Cidadão, disponibilizada pelo BANCO CENTRAL DO BRASIL (2024), o IPCA acumulado entre dez/2014 e dez/2023 é de 68,14%. Assim, para alcançar o custo por vítima fatal em 2023, multiplica-se a taxa de 1,6814 pelo custo de 2014, alcançando um custo por óbito de R$ 728.528,24.
Por fim, multiplicando o custo individual das mortes em 2023 pela quantidade estimada de óbitos de 34.631, tem-se que o custo total dos óbitos previstos no trânsito em 2023 é de R$ 25.229.661.499,04, ou aproximadamente R$ 25,2 bilhões.
6 Conclusão
Os modelos regressivos desenvolvidos antecipam uma tendência ao aumento relativo nas vítimas de sinistros de trânsito em 2023, uma revelação preocupante à presente situação da segurança viária no Brasil. Em contrapartida, os modelos de séries temporais antecipam uma possível diminuição, provavelmente devido a sensibilidade desses tipos de técnicas à sazonalidade. Por isso, a análise de regressão permanece como a abordagem mais interessante no contexto do fenômeno estudado, tanto pela qualidade da previsão quanto pela capacidade explicativa deste tipo de metodologia.
Com base no modelo de regressão linear anual, que apresentou o melhor R-quadrado (\(R^2 = 0,98\)), a quantidade prevista de óbitos no trânsito brasileiro é de 34.631, representando um aumento de 737 vítimas fatais em comparação com a quantidade de 2022, que foi de 33.894. Traduzindo esses valores em taxas de óbitos por 100 mil habitantes, o valor previsto para 2023 é de 17,05 óbitos por 100 mil habitantes, um aumento em comparação com a taxa observada em 2022, que foi 16,69 óbitos por 100 mil habitantes. Considernado o modelo de regressão linear trimestral (\(R^2 = 0,91\)), a quantidade trimestral de óbitos previstos para o primeiro trimestre de 2023 é de 8.271, um aumento de 5% em relação com o valor observado no primeiro trimestre de 2022: 7.862 óbitos.
Com a estimativa dos custos dos óbitos realizada, foi possível chegar a um valor aproximado de R$ 25 bilhões com base nos 34.631 previstos, ou seja, aproximadamente R$ 730 mil por óbito.
É fundamental também destacar que as soluções de segurança viária não dependem apenas de atributos da mobilidade urbana. Inúmeros fatores socioeconômicos e de infraestrutura podem afetar o desempenho da segurança. O cenário atual da segurança viária brasileira apresenta alguns desafios e deficiências que podem impactar na conquista das metas de redução estabelecidas em âmbito nacional pelo PNATRANS. Os dados previstos mostram um desempenho abaixo do ideal no combate da fatalidade no trânsito brasileiro, conferindo uma perspectiva pessimista para a década atual no Brasil e, caso este cenário não seja amenizado com antecedência, é improvável a ocorrência de avanços significativos nos objetivos da Segunda Década de Ação pela Segurança no Trânsito.
Referências
AL-GHAMDI, A. S. Time Series Forecasts for Traffic Accidents, Injuries, and Fatalities in Saudi Arabia. Journal of King Saud University - Engineering Sciences, v. 7, n. 2, p. 199–217, 1995.
ANDRADE, F. R. D.; ANTUNES, J. L. F. Tendência do número de vítimas em acidentes de trânsito nas rodovias federais brasileiras antes e depois da Década de Ação pela Segurança no Trânsito. Cadernos de Saúde Pública, v. 35, n. 8, p. e00250218, 2019.
BANCO CENTRAL DO BRASIL. SGS - Sistema Gerenciador de Séries Temporais - v2.1. 8 dez. 2023.
BANCO CENTRAL DO BRASIL. Calculadora Do Cidadão. Disponível em: <https://www3.bcb.gov.br/CALCIDADAO/publico/exibirFormCorrecaoValores.do?method=exibirFormCorrecaoValores>. Acesso em: 11 abr. 2024.
BLUMENBERG, C. et al. Is Brazil going to achieve the road traffic deaths target? An analysis about the sustainable development goals. Injury Prevention, v. 24, n. 4, p. 250–255, ago. 2018.
CAI, H.; ZHU, D.; YAN, L. 2015 International Conference on Transportation Information and Safety (ICTIS). Wuhan, China: IEEE, jun. 2015. Disponível em: <http://ieeexplore.ieee.org/document/7232140/>
CARVALHO, C. H. R. Custos Do Acidentes de Trânsito No Brasil: Estimativa Simplificada Com Base Na Atualização Das Pesquisas Do IPEA Sobre Custos de Acidentes Nos Aglomerados Urbanos e Rodovias. [s.l.] Instituto de Pesquisa Econômica Aplicada, 2020. Disponível em: <https://www.ipea.gov.br/portal/images/stories/PDFs/TDs/td_2565.pdf>.
CONSELHO NACIONAL DE TRÂNSITO. RESOLUÇÃO CONTRAN Nº 870. 11 jan. 2018.
CONSELHO NACIONAL DE TRÂNSITO. RESOLUÇÂO CONTRAN N° 1004. 21 dez. 2023.
FERRAZ, A. C. P. et al. Segurança no trânsito. 3. ed. Curitiba, PR: [s.n.].
HYNDMAN, R. J.; KHANDAKAR, Y. Automatic Time Series Forecasting: The forecast Package for R. Journal of Statistical Software, v. 27, n. 3, 2008.
JAFARI, S. A. et al. Prediction of road traffic death rate using neural networks optimised by genetic algorithm. International Journal of Injury Control and Safety Promotion, v. 22, n. 2, p. 153–157, 3 abr. 2015.
JAMES, G. et al. An introduction to statistical learning: with applications in R. Second edition ed. New York, NY: Springer, 2021.
JIN, X.; ZHENG, J.; GENG, X. Prediction of Road Traffic Accidents Based on Grey System Theory and Grey Markov Model. International Journal of Safety and Security Engineering, v. 10, n. 2, p. 263–268, 30 abr. 2020.
MINISTÉRIO DA INFRAESTRUTURA. Plano Nacional de Redução de Mortes e Lesões no Trânsito. 11 jan. 2018.
MINISTÉRIO DA SAÚDE. Mortalidade desde 1996 pela CID-10. 25 set. b2023.
MINISTÉRIO DA SAÚDE. População residente. 25 set. a2023.
MINISTÉRIO DOS TRANSPORTES. Frota de Veículos - 2022. 25 set. b2023.
MINISTÉRIO DOS TRANSPORTES. Registro Nacional de Condutores Habilitados. 25 set. a2023.
POLÍCIA RODOVIÁRIA FEDERAL. Dados Abertos da PRF. 23 set. 2023.
RODRÍGUEZ, J.; JATTIN, J.; SORACIPA, Y. Probabilistic temporal prediction of the deaths caused by traffic in Colombia. Mortality caused by traffic prediction. Accident Analysis & Prevention, v. 135, p. 105332, fev. 2020.
SALDANHA, R. Microdatasus: pacote para download e pré-processamento de microdados do Departamento de Informática do SUS (DATASUS). [s.l: s.n.].
SENETA, E. Markov and the Birth of Chain Dependence Theory. International Statistical Review / Revue Internationale de Statistique, v. 64, n. 3, p. 255, dez. 1996.
SHUMWAY, R. H.; STOFFER, D. S. Time series analysis and its applications: with R examples. Fourth edition ed. Cham: Springer, 2017.
WORLD HEALTH ORGANIZATION. Global status report on road safety 2023. [s.l: s.n.].
ZHONG-XIANG, F. et al. Combined Prediction Model of Death Toll for Road Traffic Accidents Based on Independent and Dependent Variables. Computational Intelligence and Neuroscience, v. 2014, p. 1–7, 2014.